PC 算法

把大三的时候在实验室摸鱼看贝叶斯网络和 PC 算法时写的笔记整理到这里来，免得哪天我换电脑时把笔记搞没了。

这里是当时写的 PC 算法的 Python 实现： Renovamen/pcalg-py

# 概率图模型

对于一个 $K$ 维随机向量 $X=[X_1,X_2,\dots ,X_K{]}^{\top }$，一般难以直接建模。因为如果每个变量为离散变量并有 $M$ 个可能取值，在不作任何独立性假设的前提下，需要 $M^K-1$ 个参数才能表示其概率分布，参数数量会非常庞大。

一种减少参数数量的方法是独立性假设。把 $X$ 的联合概率分解为 $K$ 个条件概率的乘积：

$$p(X=x)=\prod _{k=1}^{K}p(x_k|x_1,\dots ,x_{k-1})$$

$x$ 为随机向量 $X$ 的取值。可以看到，如果某些变量之间存在条件独立，参数数量就可以大幅减少。

因此，概率图模型（Probabilistic Graphical Model，PGM）用图结构来描述多元随机变量之间的条件独立关系，从而为研究高维空间中的概率模型带来了很大的便捷。

概率图模型中，每个节点表示一个（或一组）随机变量，边表示这些随机变量之间的概率依赖关系。常见的概率图模型可以分为有向图模型和无向图模型。

• 有向图模型（Directed Graphical Model），也称为贝叶斯网络（Bayesian Network）或信念网络（Belief Network），使用有向无环图（Directed Acyclic Graph，DAG）来描述变量之间的关系。如果两个节点之间有连边，表示这两个变量之间有因果关系，即不存在其他变量使得这两个变量条件独立。

• 无向图模型，也称为马尔可夫随机场（Markov Random Field，MRF），使用无向图来描述变量之间的关系。两个节点之间有连边代表这两个变量之间有概率依赖关系，但不一定是因果关系。

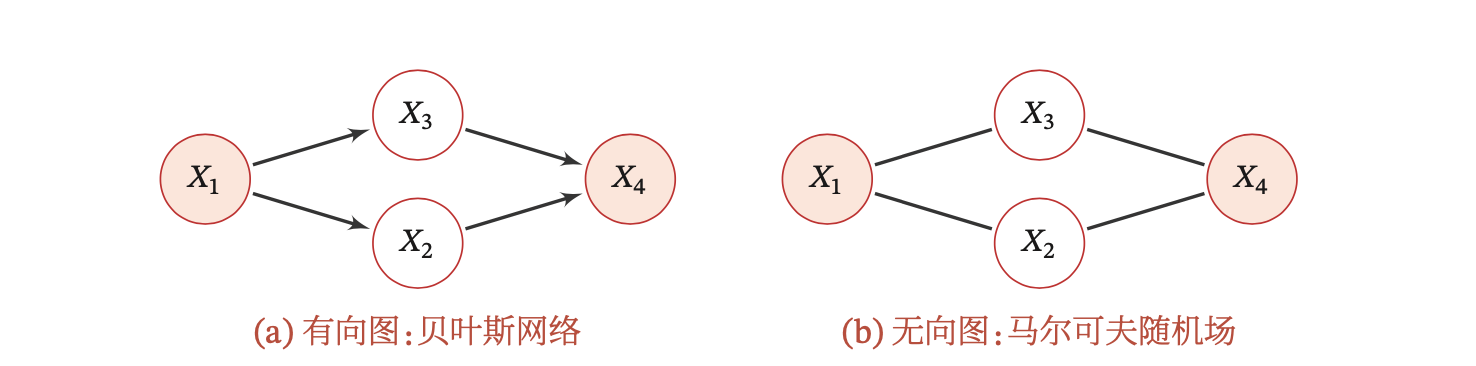
图片来源：《神经网络与深度学习》，邱锡鹏

本文只讨论有向图模型，即贝叶斯网络。

# 贝叶斯网络

# 定义

有向无环图 $G$ 中，每个节点对应 $K$ 维随机向量 $X$ 中的一个变量，有向边 $e_{ij}$ 表示随机变量 $X_i$ 和 $X_j$ 之间具有因果关系，父节点 $X_i$ 是『因』，子节点 $X_j$ 是『果』，显然这两个点之间一定非条件独立。

令 $X_{{\pi }_k}$ 为变量 $X_k$ 的所有父节点变量集合，$P(X_k\mid X_{{\pi }_k})$ 表示每个随机变量的局部条件概率分布（Local Conditional Probability Distribution）。

如果 $X$ 的联合概率分布可以分解为每个随机变量 $X_k$ 的局部条件概率的连乘形式，即：

$$p(x)=\prod _{k=1}^{K}p(x_k\mid x_{{\pi }_k})$$

那么称 $(G,X)$ 构成了一个贝叶斯网络。

# 局部马尔可夫性质

每个随机变量在给定父节点的情况下，条件独立于它的非后代节点：

$$X_k\perp \perp Z\mid X_{{\pi }_k}$$

其中 $Z$ 为 $X_k$ 的非后代节点。

# 基本问题

• 学习问题

  • 结构学习：那么怎样才可以获得这个神奇的有向无环图呢，这就是结构学习问题。即学习出最优网络结构，也就是各节点之间的依赖关系。主流的结构学习方法主要可以分为：

    • 基于评分搜索的方法：利用搜索算法和评分函数，对每一个搜索到的网络结构进行评分，最终搜索出评分最高的网络结构。搜索算法的复杂度和精确度直接决定了学习算法的搜索效率，评分函数的优劣也直接决定了算法的计算复杂度和精确度。所以选择合理的优化搜索算法和评分函数是该类方法的核心问题。

      该类方法容易陷入局部最优解而无法达到全局最优，并且结构空间的⼤⼩随节点的增加呈指数增加(空间复杂度)。

    • 基于依赖统计分析的方法：分析变量间的依赖关系，在依赖性较大的两节点之间添加连接边，得到无向图。然后根据包含关系等方式确定无向图中边的方向，得到最终的有向无环图。本文要讨论的 PC 算法就是这类方法中（比较古老）的一种。

      该类方法能获得全局最优解，但随着节点的增加，算法的时间复杂度会增加得很快；并且它不能区分同属于一个马尔可夫等价类的图，这一点后面会讲到。

  • 参数学习：在给定网络结构时，确定网络参数，即参数估计问题：

    • 不含隐变量：如果图模型中不含隐变量（latent variable），即所有变量都是可观测的，那么网络参数一般可以直接通过最大似然来进行估计。

    • 含隐变量：有些时候 $X$ 中的变量有很复杂的依赖关系，这时通常会引入隐变量 $z$ 来简化模型。如果图模型中包含隐变量，即有部分变量是不可观测的，这时就需要用 EM 算法（Expectation Maximum，期望最大化算法）来进行参数估计。

      如果 EM 算法中的后验是 intractable 的，那么又需要用变分推断（Variational Inference）来寻找一个简单分布来近似后验。

      而在深度学习大行其道的今天，你可能会想到用神经网络去拟合这个后验不就完事儿了，是的这就是变分自编码器（Variational Auto-Encoder，VAE）的思想，去学它吧朋友。

    本文不讨论参数学习问题，但我在我的笔记本上写了一些参数学习相关的东西，有兴趣的话可以看一看。

• 推断问题：在已知部分变量时，计算其他变量的条件概率分布

# PC 算法

好的现在讲主题了，用 PC 算法^[1]来学习出贝叶斯网络的结构。如上文所述，PC 算法会先确定节点间的依赖关系（但不确定方向），即先生成一个无向图，然后再确定依赖方向，把无向图扩展为完全部分有向无环图（Completed Partially Directed Acyclic Graph，CPDAG）。

# 依赖关系确立

设 $V$ 是输入点集，有以下步骤：

• 在 $V$ 上生成完全无向图 $G$
• 对于 $G$ 中的两个相邻点 $i,j$，如果 $i$ 和 $j$ 能在给定节点 $k$ 时条件独立，则删除 $i$ 和 $j$ 之间的边

这样会得到一个无向图，图中的无向边表示它连接的两个节点之间有依赖（因果）关系，这样的无向图叫骨架（skeleton）。PC 算法把上述过程转化为了 $d$ 分隔（d-separation）^[2]问题。

# d 分隔

用 $O(i,j)$ 表示能够 $d$ 分隔 $i$ 和 $j$ 的点集，用 $adj(G,x)$ 表示图 $G$ 中节点 $x$ 的相邻点集，那么 PC 算法检验条件独立性的具体流程为^[3]：

Estimating High-Dimensional Directed Acyclic Graphs with the PC-Algorithm. Markus Kalisch and Peter Buhlmann. JMLR 2007.

简单总结一下：

• $\ell =1$

• repeat

  • for 每个相邻点对 $(i,j)$

    • for $adj(G,i)\backslash \{j\}$ 或 $adj(G,i)\backslash \{i\}$ 的所有可能的节点数为 $\ell$ 的子集 $K$

      • 测试 $K$ 能否 $d$ 分隔 $(i,j)$

      • 如果能，说明 $i$ 和 $j$ 之间不存在有效的依赖关系，所以删除边 $i-j$，并将这个点集加入 $O(i,j)$ 和 $O(j,i)$，break

  • $\ell =\ell +1$

• until 当前图中的所有的邻接点集都小于 $\ell$

# Fisher Z Test

为了判断 $d$ 分隔，我们需要对任意两个节点进行条件独立性检验，PC 算法采用了 Fisher Z Test^[4] 作为条件独立性检验方法。实际上 Fisher Z Test 是一种相关性检验方法，但 PC 算法认为这一堆随机变量整体上服从多元高斯分布，这时变量条件独立与变量之间的偏相关系数为 0 等价（多元高斯分布的基本特性，证明过程可以参考 Steffen L. Lauritzen 的课件^[5]第 4.2.1 节），所以可以用 Fisher Z Test 进行条件独立性检验。

偏相关系数指校正其它变量后某一变量与另一变量的相关关系，校正的意思可以理解为假定其它变量都取值为均数。任意两个变量 $i,j$ 的 $h$ 阶（排除其他 $h$ 个变量的影响后，$h<=k-2$）偏相关系数为：

$${\rho }_{i,j\mid K}=\frac{{\rho }_{i,j\mid K\backslash h}-{\rho }_{i,h\mid K\backslash h}{\rho }_{j,h\mid K\backslash h}}{\sqrt{(1-{\rho }_{i,h\mid K\backslash h}^2)(1-{\rho }_{j,h\mid K\backslash h}^2)}}$$

为了判断 $\rho$ 是否为 0，需要将 $\rho$ 通过 Fisher Z 变换^[6]转换成正态分布：

$$Z(i,j\mid K)=\frac{1}{2}\log (\frac{1+{\hat{\rho }}_{i,j\mid K}}{1-{\hat{\rho }}_{i,j\mid K}})$$

定义零假设和对立假设：

• 零假设：$H_0(i,j\mid K):{\rho }_{i,j\mid K}\ne 0$
• 对立假设：$H_1(i,j\mid K):{\rho }_{i,j\mid K}=0$

然后给定一个显著性水平 $\alpha \in (0,1)$，那么（双侧）检验的规则为，如果有：

$$\sqrt{n-|K|-3}|Z(i,j\mid K)\le {\Phi }^{-1}(1-\alpha /2)$$

其中 $\Phi (\cdot )$ 为 $\mathcal{N}(0,1)$ 的累积分布函数，则拒绝零假设，$i,k$ 关于 $K$ 条件独立。所以将上面伪代码的第 11 行替换为 if $\sqrt{n-|K|-3}|Z(i,j\mid K)\le {\Phi }^{-1}(1-\alpha /2)$。

# 依赖关系方向确立

经过上一个阶段，我们得到了一个无向图。现在我们要利用 $d$ 分隔的原理来确定图中边的依赖方向，把骨架扩展为 DAG。

对于任意三个以有效依赖关系边相连的节点 $X-Z-Y$，其依赖关系必为下图的四种关系之一：

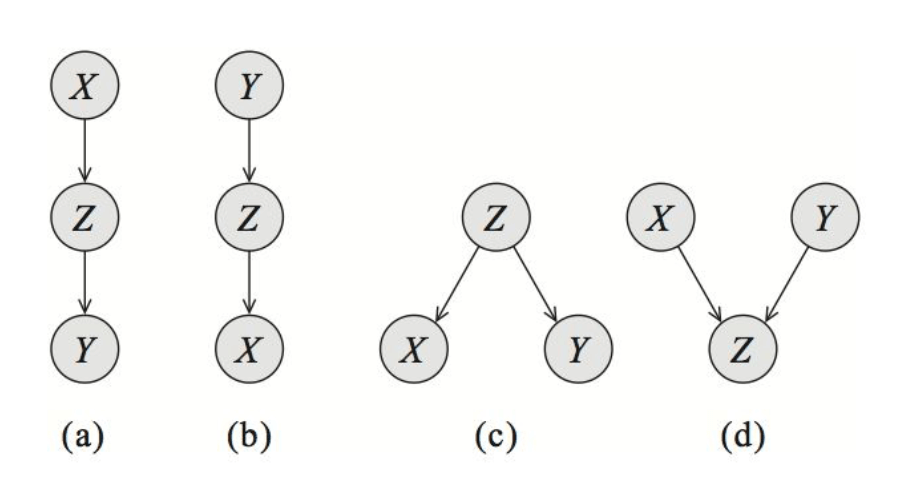
$d$ 分隔的结论为：对于有向无环图 $E$，有两个节点 $X,Y$ 和一个点集 $O$，为了判断 $X$ 和 $Y$ 是否关于 $O$ 条件独立，考虑 $E$ 中所有 $X$ 和 $Y$ 之间的无向路径，对于其中一条路径，如果它满足以下两个条件中的任意一条，则称这条路径是阻塞的：

• 路径中存在某个节点 $Z$ 是 head-to-tial（图中情况 a, b）或 tail-to-tail 节点（图中情况 c），且 $Z$ 包含在 $O$ 中
• 路径中存在某个节点 $Z$ 是 head-to-head 节点（图中情况 d），且 $Z$ 没有被包含在 $O$ 中

如果 $X,Y$ 间所有的路径都是阻塞的，那么 $X,Y$ 关于 $O$ 条件独立；否则，$X,Y$ 不关于 $O$ 条件独立。

而我们已经记录了 $d$ 分隔 $X$ 和 $Y$ 的点集 $O$，因此我们可以由 $d$ 分隔的结论反推出贝叶斯网络中边的方向，方向的判断方法可以转换成以下三条规则：

• 规则 1：如果存在 $X\to Y-Z$，把 $Y-Z$ 变为 $Y\to Z$
• 规则 2：如果存在 $X\to Z\to Y$，把 $X-Y$ 变为 $X\to Y$
• 规则 3： 如果存在 $X-Z_1\to Y$，$X-Z_2\to Y$，且 $Z_1,Z_2$ 不相邻，把 $X-Y$ 变为 $X\to Y$

实际上还可以推出一个规则 4：

• 规则 4：如果存在 $X-Z_1\to Z_2$ 和 $Z_1\to Z_2\to Y$，且 $Z_1,Z_2$ 不相邻，把 $X-Y$ 变为 $X\to Y$

但很显然这种情况是矛盾的，不可能存在，所以不用考虑。

总结一下：

Estimating High-Dimensional Directed Acyclic Graphs with the PC-Algorithm. Markus Kalisch and Peter Buhlmann. JMLR 2007.

这样我们就可以得到一个完全部分有向无环图。

# 马尔科夫等价类

很明显，完全部分有向无环图（CPDAG）跟有向无环图看上去就不一样。首先来看什么是部分有向无环图（Partially Directed Acyclic Graph，PDAG）：

而完全部分有向无环图指：

关于可逆和不可逆：

换句话说用 PC 算法得到的图是含有无向边的。这是因为依据 $d$ 分隔确定的条件独立性所构造的网络 结构不具有唯一性，它们只是真实的贝叶斯网络的马尔科夫等价类（Markov Equivalence Class）：

举个栗子：

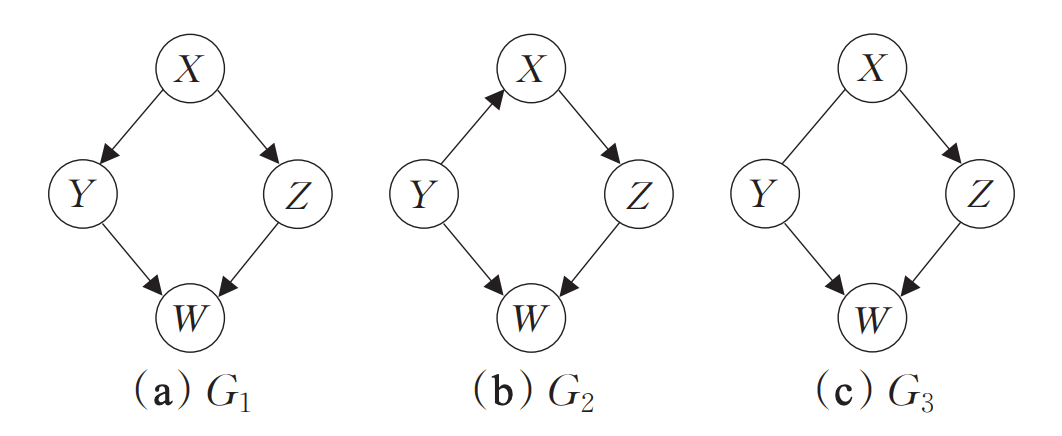
马尔科夫等价类

上图 $G_1$ 和 $G_2$ 是马尔科夫等价类，它们左上角的那条有向边方向并不相同，这时 PC 算法就无法判断这条边的方向了，只能输出无向边，即 $G_3$。

所以，严格来说，PC 算法以及大多数基于依赖统计分析的贝叶斯网络结构学习算法，得到的都只是一个 CPDAG（依然有无向边），而不是真正意义上的贝叶斯网络（有向无环图）。

# 参考